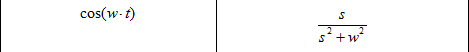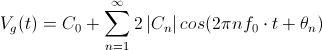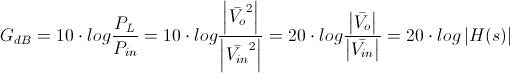Hemos dedicado esta semana al estudio de la respuesta de los circuitos en función de la frecuencia de su excitación, es decir al análisis de la respuesta frecuencial de los circuitos. Para ello, hemos introducido dos nuevos conceptos: los diagramas polos-ceros y los trazados de Bode.
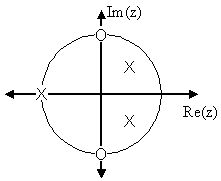
De entrada, hemos aclarado que siempre reconduciremos las funciones de red a cocientes de polinomios en s. De esta manera, podremos factorizar tanto el numerador como el denominador para encontrar los valores de s (y por tanto de ω) que anulan uno u otro. En el caso del numerador, estos valores harán que la función de red valga cero, mientras que las raíces del denominador harán que la función presente sus valores máximos. Por este motivo, llamaremos a las raíces del numerador ceros y a las del denominador polos. Situándolas en el plano complejo y representándolas con círculos y cruces respectivamente, obtenemos lo que se conoce como un diagrama polos-ceros, que nos permite encontrar rápidamente las pulsaciones que provocan uno u otro efecto en el circuito.
Por otra parte, hemos destacado la utilidad de representar la amplificación de un circuito en función de su frecuencia. A este respecto, parece interesante hacer esta representación en una escala logarítmica, tal como sugirió Hendrik Wade Bode, ingeniero eléctrico estadounidense.
¿Por qué? Si tomamos el cociente entre las potencias de entrada y salida, veremos que, si Rin y RL son iguales, es igual al cuadrado del cociente entre las tensiones de entrada y salida. Si tomamos diez veces el logaritmo de esta expresión como la ganancia del circuito, el exponente 2 pasa a multiplicar al número 10. Por lo tanto, la expresión que nos queda es que la ganancia del circuito, en dB, es 20 veces el logaritmo de la función de red.
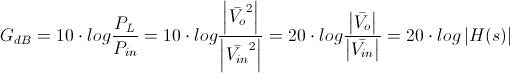
Por lo tanto, representaremos la ganancia en dB en función del logaritmo de la frecuencia. Esto significa que las frecuencias que se encuentren separadas por una misma distancia serán proporcionales en un factor 10, es decir, las separará una década. A este respecto, entenderemos el número de décadas entre dos frecuencias como el «número de factores 10 entre ellas», es decir, el logaritmo del cociente entre una y otra. Análogamente, entenderemos por octava la separación entre dos frecuencias proporcionales en un factor 2, y el número de octavas entre dos frecuencias será el logaritmo en base 2 del cociente entre ambas. De estas dos definiciones podremos extraer que el número de décadas es log 2 veces el de octavas, aproximadamente 0,3.
En cuanto al argumento de la función de red, lo representaremos de la misma manera: en función del logaritmo de la pulsación.
La utilidad de trabajar con logaritmos, y por tanto la utilidad de realizar este tipo de representación, radica en que el logaritmo de un producto o cociente es la suma o resta, respectivamente, de los factores. De esta manera, y recordando lo que hemos dicho al inicio, si descomponemos la función de red en factores elementales que sepamos representar individualmente, la curva final de respuesta será la suma punto por punto de todos estos trazados. Es por esto por lo que hemos aprendido esta semana a representar los factores elementales que pueden componer H(s): para poderlos identificar fácilmente y poder construir rápidamente curvas de respuesta frecuencial.
H(s) = k / s
La gráfica correspondiente a la ganancia de un circuito con una función de red de este tipo es una recta de pendiente -20 db/década, que corta al eje de abscisas en ω=k. En cuanto a su fase, valdrá -π/2. Con k = 1:

H(s) = k·s
De manera complementaria al caso anterior, una función de red de este tipo presenta una ganancia cuya gráfica es una recta. En este caso, es de pendiente positiva de valor 20 dB/década y, de nuevo, corta al eje de abscisas en x = k. Por otra parte, su argumento es π/2. Con k = 1:

H(s) = 1 / (s/ωc + 1)
La ganancia de un circuito cuya función de res es de este tipo es de 0 dB hasta ω = ωc. A partir de este punto, su comportamiento se puede aproximar por una recta de pendiente -20 dB/década. Esta aproximación, denominada asintótica, tiene el ligero inconveniente de que no acierta en ω = ωc. Para este valor, la ganancia es de -3 dB. Sin embargo, la tangencia a las asíntotas se produce muy rápidamente, por lo que la consideraremos una aproximación válida.
En cuanto a su fase, la podemos aproximar por 0 hasta ω = ωc, y por -π/2 para valores superiores a ωc. Sin embargo, en este caso la aproximación no es en absoluto precisa, ya que en ω = ωc el argumento de la función de red es -π/4. También hemos observado que la tangencia con las asíntotas se produce en el intervalo de una década. Por lo tanto, corregiremos la aproximación asintótica anterior añadiendo un tramo de pendiente -π/4 rad/década entre las frecuencias situadas una década por encima y por debajo de ωc. Siendo T el periodo asociado a la pulsación ωc:

Vemos que este circuito tiene la característica de atenuar las señales cuya frecuencia es mayor que ωc, a la vez que deja pasar las señales de frecuencia menor. Diremos, por lo tanto, que se comporta como un filtro paso-bajo, y definiremos el ancho de banda como el intervalo de frecuencias que atraviesan el circuito con una atenuación máxima de -3 dB, esto es, que la tensión de salida sea como mínimo 0.707 veces la de la entrada.
Huelga decir que el factor 1/ωc + 1 tendrá una representación opuesta: su ganancia es de 0 dB hasta ωc, donde vale +3 dB, y a partir de este valor crece a razón de 20 dB / década. Su fase será de 0 rad hasta la frecuencia una década inferior a ωc, donde crece a π/4 rad/década hasta la frecuencia una década superior a ωc. A partir de este valor, permanece constante en π/2.
H(s) = ωo² / (s² + 2·ρ·ωo·s + ωo²)
Estudiando polinomios de segundo orden, hemos visto que siempre los podremos reconducir a una expresión similar a la del denominador de esta función de red. Lo interesante de escribirlos de esta manera es que, aplicando la fórmula que conocemos desde la ESO, encontraremos que sólo tiene raíces reales para ρ > 1. En estos casos, podremos factorizarlo y expresar la función de red como producto de dos expresiones del tipo 1 / (s/ωc + 1). Sin embargo, para 0 < ρ < 1 las raíces del polinomio serán complejas, y lo dejaremos expresado como polinomio de segundo orden.
Al analizar la ganancia de circuitos con este tipo de funciones de red, observamos que, asintóticamente, la ganancia vale 0 dB para ω < ωo, y decrece a razón de -40 dB/década para ω > ωo. Sin embargo, esta aproximación falla a ω = ωo. A esta pulsación, la ganancia vale -20·log 2ρ.
Dos valores interesantes de ρ son 0.707 y 0.5. Para ρ = √2/2 = 0.707, la ganancia es de -3dB, por lo que diremos que el circuito se comporta como un filtro paso-bajo de segundo orden. Para ρ = 0.5, la ganancia es de 0 dB. Por lo tanto, para ρ < 0.5 el circuito presentará una ganancia positiva a ω = ωc, lo que se conoce como un pico de resonancia. Esto nos será muy útil para diseñar circuitos enormemente sensibles a una cierta frecuencia, como lo son los sintonizadores de radio. El trazado de Bode de ganancia de un circuito cuya H(s) es de este tipo presenta por tanto una forma tal que así:
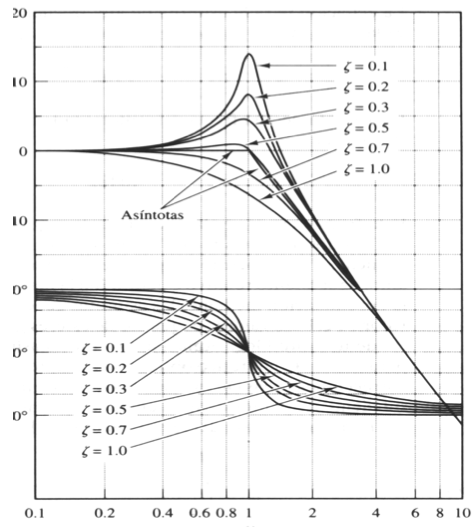
Vemos también que el argumento de la función de red vale 0 para ω < ωo, y que para valores superiores vale -π. Aunque la forma de la curva depende también del factor ρ, la aproximaremos de nuevo por una recta de pendiente -π/2 rad/década entre las frecuencias situadas una década por debajo y por encima de ωo.
Tal como lo hicimos con los filtros paso-bajo, definiremos en este caso el ancho de banda como el intervalo de frecuencias que experimentan una amplificación de al menos 3 dB por debajo de la máxima amplificación del pico (esto es, si el pico es de 64 dB, el ancho de banda es el intervalo de frecuencias que son amplificadas al menos 61 dB). Hemos visto que, siempre que ρ < 0.1, las frecuencias de corte superior e inferior (las que delimitan el ancho de banda) son ωo ± 2ρ.
ωci = ωo – 2ρ
ωcs = ωo + 2ρ
Hemos definido también una medida para conocer la precisión o selectividad de un pico de resonancia, y la hemos llamado factor de calidad Q. Es el cociente entre la frecuencia ωo y el ancho de banda, ya que construir un resonador con el mismo ancho de banda pero a una frecuencia de resonancia mucho mayor es más difícil. Por otra parte, un resonador con la misma frecuencia de resonancia que otro pero mayor ancho de banda será de peor calidad.
Q = ωo / BW
Por último, hemos definido el dBμV como 20 veces el logaritmo del cociente entre una tensión y un microvatio (de manera análoga a como describimos el dBm para la potencia). De esta manera, la tensión de salida, expresada en dBμV, será igual a la tensión de entrada, también expresada en dBμV más la ganancia del circuito a esa determinada frecuencia, también expresada en dB. Esto nos simplificará la obtención de tensiones de salida y entrada.
Vo (dBμV) = Vg (dBμV) + G (dB)